algebra: ecuaciones cuadraticas

ecuaciones cuadraticas.

Podemos resolver cualquier ecuación cuadrática completando el cuadrado — convirtiendo un polinomio en un trinomio cuadrado perfecto. Si completamos el cuadrado en la ecuación genérica y luego resolvemos x, encontramos que 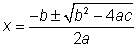.  Esta ecuación un poco extraña se conoce como fórmula cuadrática.

Esta fórmula es muy útil para resolver ecuaciones cuadráticas que son difíciles o imposibles de factorizar, y usarla puede ser más rápido que completar el cuadrado. La fórmula cuadrática puede ser usada para resolver cualquier ecuación cuadrática de la forma .

Derivando la Fórmula Cuadrática

Vamos a completar el cuadrado en la ecuación general, , para ver exactamente cómo se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado:

·         Empezar con una ecuación de la forma .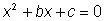

·         Reescribir la ecuación de forma que 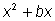 quede despejada.

·         Completar el cuadrado sumando 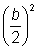a ambos lados.

·         Reescribir como el cuadrado de un binomio y resolver x.

¿Puedes completar el cuadrado en la ecuación cuadrática general ? Inténtalo antes de continuar con el siguiente ejemplo. Pista: Cuando trabajas con la ecuación general , existe una complicación que consiste en que el coeficiente de 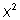 no es igual a 1. Puedes dividir la ecuación entre a, lo que hace que se compliquen algunas de las expresiones, pero si tienes cuidado, todo resultará bien, y al final, ¡obtendrás la fórmula cuadrática!

Ejemplo
Problema	Completar el cuadrado de  para obtener la fórmula cuadrática.
			Dividir ambos lados de la ecuación entre a, para que el coeficiente de  sea 1
			Reescribir de tal forma que el lado izquierdo tenga la forma  (aunque en este caso bx es ).
			Sumar  a ambos lados para completar el cuadrado
			Escribir el lado izquierdo como un binomio cuadrado
			Evaluar como .
			Escribir las fracciones del lado derecho usando un común denominador
			Sumar las fracciones de la derecha
			Sacar la raíz cuadrada de ambos lados. ¡Recuerda que debes conservar ambas raíces la positiva y la negativa!
			Restar  de ambos lados para despejar x.
			El denominador bajo el radical es un cuadrado perfecto, entonces .
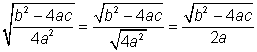			Sumar las fracciones ya que tienen un común denominador
Solución

Y ahí la tenemos, la fórmula cuadrática.

Resolviendo una Ecuación Cuadrática usando la Fórmula Cuadrática

La fórmula cuadrática funcionará para cualquier ecuación cuadrática, pero sólo si la ecuación está en su forma estándar, . Para usarla, sigue los siguientes pasos:

·         Primero transforma la ecuación a la forma estándar

·         Identifica los coeficientes, a, b, y c. Ten cuidado de incluir los signos negativos si los términos bx o c están siendo restados.

·         Sustituye los valores de los coeficientes en la fórmula cuadrática

·         Simplifica lo más posible.

·         Usa el ± enfrente del radical para separar la solución en dos valores: uno en el que la raíz cuadrada se suma, y el otro donde la raíz cuadrada se resta.

·         Simplificar ambos valores para obtener las posibles soluciones.

Son bastantes pasos. Vamos a intentarlo:

Ejemplo
Problema	Usar la fórmula cuadrática para resolver la ecuación
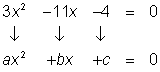			a = 3, b = -11,  c = -4 Nota que la resta de signos significa que los coeficientes b y c son negativos
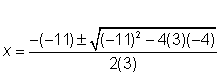			Sustituir los valores en la fórmula cuadrática
			Simplificar, teniendo cuidado con los signos
			Simplificar más
			Simplificar el radical: .
	o		Separar y simplificar para encontrar las soluciones de la ecuación cuadrática. Nota que en una, 13 es sumado y en la otra, 13 es restado
Solución	x = 4 o